Правильная Шестиугольная Пирамида Макет
Напоминаем, что в соответствии с профстандартом педагога (утверждён Приказом Минтруда России), если у Вас нет соответствующего преподаваемому предмету образования, то Вам необходимо пройти профессиональную переподготовку по профилю педагогической деятельности. Сделать это Вы можете дистанционно на сайте проекта 'Инфоурок' и получить диплом с присвоением квалификации уже через 2 месяца! Только сейчас действует СКИДКА 50% для всех педагогов на все 111 курсов профессиональной переподготовки!
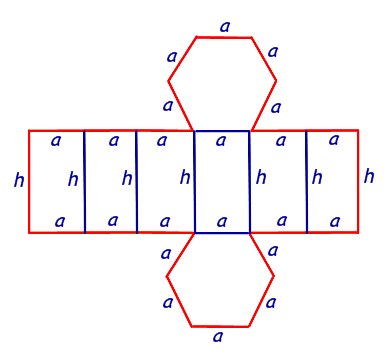
Как и на сколько обманывают в такси CityMobil (Мск). Развертка пирамиды. Как построить развертку шестиугольной пирамиды. Автор: Moroz. Дата: 2015-01-19. Если вам нужна пошаговая инструкция как построить развертку пирамиды, то прошу к нашему уроку. Первым делом оцените, развернута ли ваша пирамида аналогичным образом, как на рисунке 1. Повторив данные действия необходимое количество раз (все зависит от того, сколько граней у вашей пирамиды) мы получим такой вот веер (рисунок 3). При правильном построении вы должны получить все точки основания, причем крайние должны повториться. Это требуют не всегда, но все же оно нужно: добавить основание пирамиды к развертке боковой поверхности. Правильная шестиугольная пирамида. В правильной шестиугольной пирамиде SABCDEF, стороны основания которой равна 1, а боковые ребра равны 2, найдите расстояние от точки С до прямой SF. Объем треугольной пирамиды, являющейся частью правильной шестиугольной пирамиды, равен. Найдите объем шестиугольной пирамиды. Макеты правильных выпуклых многогранников, таких как додекаэдр и икосаэдр, также можно выполнить в виде развертки на плоскости и собрать в объем. Шестиугольная: в основании – правильный шестиугольник, вершина проецируется в центр основания. Объем правильной шестиугольной пирамиды. Пусть сторона основания равна, а боковое ребро.
Доступна рассрочка с первым взносом всего 10%, при этом цена курса не увеличивается из-за использования рассрочки! Конспект урока по геометрии в 10 классе на тему: Правильная пирамида Цели урока: образовательные: ввести понятие правильной пирамиды; доказать теорему о площади боковой поверхности правильной пирамиды; рассмотреть задачи, связанные с правильной пирамидой. Развивающие: способствовать развитию логического мышления, математической речи учащихся, внимания, памяти; воспитательные: воспитание интереса к математике как учебному предмету через современные технологии преподавания; способствовать развитию навыков самоконтроля; Оборудование: учебник, конспект. Тип урока: Урок изучения новых знаний и умений. Ход урока. Организационный момент Приветствие.
Проверка готовности. Актуализация опорных знаний Демонстрация модели правильной пирамиды, в ходе которого производится опрос учащихся о всех свойствах данной фигуры. Целеполагание В ходе опроса ученики сообщают тему и цель урока. Объяснения нового материала Пирамида называется правильной, если в основании - правильный многоугольник, а отрезок, соединяющий вершину с центром основания, является ее высотой.

Пирамида Геометрия
Любое боковое ребро представляет собой гипотенузу прямоугольного треугольника, одним катетом которого служит высота пирамиды, а другим - радиус описанной окружности около основания (показать на модели). Следовательно, боковые ребра правильной пирамиды равны друг другу, а боковые грани - равнобедренные треугольники. Основания этих треугольников равны, так как в основании правильный многоугольник.
Следовательно, боковые грани равны по третьему признаку равенства треугольников. Высота боковой грани правильной пирамиды, проведенная из вершины, называется апофемой. Все апофемы правильной пирамиды равны друг другу. Докажите теорему о площади боковой поверхности правильной пирамиды. Теорема Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему. Дано: РА 1 А 2.А n - правильная пирамида, PN - апофема. Доказать: Доказательство: (по определению правильной пирамиды).
Что и требовалось доказать. Закрепление нового материала Устная работа 1. Какая пирамида называется правильной? Докажите, что боковые грани правильной пирамиды равные, боковые ребра равные. Что называется апофемой? Чему равна площадь боковой поверхности?
Решение задач № 254 (а, б), решают ученики у доски. № 264 - в сильном классе комментированием. № 254 В правильной треугольной пирамиде сторона основания равна а, высота равна Я. Найдите: а) боковое ребро пирамиды; б) плоский угол при вершине пирамиды.
Дано: DABC - пирамида, ΔАВС - равносторонний, АВ = a, DO = Н. Найти: a) DA; б ) ∠ BDC. Nobunaga`s ambition sphere of influence русификатор. Так как пирамида правильная, то AD = BD = CD. О - центр треугольника АО = R; Δ AOD - прямоугольный, OD – высота, 2. Δ BDC - равнобедренный, DK - высота, Δ DKB - прямоугольный; (Ответ: ) № 264 Найдите площадь боковой поверхности правильной шестиугольной пирамиды, если сторона основания равна а, а площадь боковой грани равна площади сечения, проведенного через вершину основания.
Дано: MABCDEF - правильная шестиугольная пирамида АВ = a, SΔAMB = SΔAMD. Найти: S 6ок. Решение: (так как пирамида правильная), так как получим Δ M ОК - прямоугольный, Δ AKO: (Ответ: 3а 2.). Подведение итогов. Рефлексия Какая была сегодня тема урока?
Какую цель ставили? Достигли цели? Расскажите по схеме, чему научились на уроке: я – знаю я – запомнил я – смог.
Домашнее задание I уровень а: п. 28,29, № 255. II уровень в: п.
28, 29, № 255. № 255 В правильной треугольной пирамиде сторона основания равна 8 см, а плоский угол при вершине равен φ. Найдите высоту пирамиды. Дано: МАВС - правильная пирамида. АВ = 8 см; ∠ CMB = φ. Решение: 1) Так как пирамида правильная, О - центр треугольника АО = R; OD = r, АО = 2О D.
2) 3) MD из Δ CDM - прямоугольный, 4) (Ответ: ). Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение редакции может не совпадать с точкой зрения авторов.
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако редакция сайта готова оказать всяческую поддержку в решении любых вопросов связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Ем доширак опять, меня некому ругать Теперь моя постель - это просто кровать. Мы разошлись как в море корабли, И то, что было с нами - не купить за рубли. Витя ак47 да я теперь один. Да, я теперь один, ты теперь одна Как будто не было тебя, не было меня. И теперь сам себе могу сварить пельмени, Пришли мои друзья, ты их звала - олени.
Правильная треугольная пирамида, вписанная в шар АQ = ВQ = CQ = SQ= R – радиус шара. AO = BO = CO = r – радиус круга, описанного около основания пирамиды. SO = H – высота пирамиды. SЕ = h – апофема пирамиды. P E T C A B R r H O S Q Правильная четырехугольная пирамида, вписанная в шар AQ = BQ = CQ = DQ = = SQ = R – радиус шара. AO = BO = CO = DO = r радиус круга, описанного около основания пирамиды.
Процессоры Intel Трехзначный процессорный номер (Processor Number, или просто PN) у Intel, используемый с 2004 года вместо тактовой частоты в обозначении процессоров ряда Pentium/Celeron, в отличие от рейтинга процессоров AMD, не является технической характеристикой процессора и не имеет отношения к его производительности. Процессоры intel википедия.
SO = H – высота пирамиды. SЕ = h – апофема пирамиды. P E D C A B R r H O S Q Треугольная пирамида описана около шара E 1 Q = OQ = TQ = R – радиус шара.
EO = PO = r – радиус круга, вписанного в основание пирамиды. A B C O S P E Q E1E1 T r E1E1 E O Q S R R r r SO = H – высота пирамиды. R A B C O S D E Q E1E1 M P P1P1 Четырехугольная пирамида описана около шара E 1 Q = P 1 Q = OQ = R – радиус шара.
EO = PO = r – радиус круга, вписанного в основание пирамиды. SO = H – высота пирамиды. R EP S E1E1 P1P1 O r Задачи Шар вписан в пирамиду. Пирамида вписана в шар. Сфера вписана в конус. Куб вписан в конус.
Шар вписан в конус. A B C O S D P Q P1P1 В правильную четырехугольную пирамиду вписан шар, объем которого 32 /3. Найдите объем пирамиды, если её высота равна 6. 1) тогда 2) 3) SP 1 Q – прямоугольный, 4) SP 1 Q SOP ( Р 1 = О=90, S – общий), откуда 5) Тогда сторона основания пирамиды вдвое больше, и равна 6) Ответ: В шар, объём которого, вписана правильная четырехугольная пирамида. Найдите объём пирамиды, если её боковое ребро равно, а высота больше радиуса шара. D C A B O S Q Решение.
1)тогда 2) Пусть OQ = x, тогда из AOQ выразим сторону АО: x 3) Составим теорему Пифагора для ASO: 5 5 Откуда находим OQ = 4. 4) Тогда SO = 5+4=9, 5) В основании пирамиды квадрат, со стороной a, равной 6) Ответ: и АО = 3. 2 Площадь поверхности сферы, вписанной в конус, равна 100. Длина окружности, по которой сфера касается поверхности конуса, равна 6. Найдите радиус основания конуса. A B O S О1О1 РО2О2 1) C = 2 r = 6, тогда r = O 2 P = 3. 2) S сферы = 4 R 2 =100, тогда R = O 1 P = 5.
3) Из O 1 O 2 P по теореме Пифагора находим: 4) В O 1 PS отрезок РО 2 высота, проведенная из вершины прямого угла, значит 5) Найдем высоту конуса SO= SO 2 +O 2 O 1 +O 1 O = 2, = 11,25. 6) SО 2 Р SOВ ( О 2 = О=90, S – общий), откуда Ответ:, O S О1О1 Р Р1Р1 В конус с образующей 6 6 и высотой 12 вписан куб. Найдите объём куба. 2) a – сторона куба, тогда 3) Выразим через a: 4) SО 1 Р 1 SOР ( О 1 = О=90, S – общий), откуда a = 6. 1) Из прямоугольного SOP находим: 5) V куба = a 3 = 6 3 = 216.
Ответ: Площадь основания конуса равна площади поверхности вписанного в него шара. Найдите радиус шара, если образующая конуса равна 10. O S О1О1 Р Р1Р1 Решение. 1) Обозначим радиус шара r, а радиус основания конуса R. 2) По условию т.е. 3) SP 1 O 1 SOP ( Р 1 = О=90, S – общий), откуда SO 1 = 5, 5 5) Тогда коэффициент подобия треугольников k = ½. 2r2r 2r2r 10-2r откуда r = 3.
4) Заметим, что РР 1 = 2 r, SP 1 = 10 – 2 r, SO = 5+ r. R r 5 Ответ: Высота конуса равна 6, а объём равен 144. Найдите площадь полной поверхности куба, вписанного в конус Шар объём которого равен 32 /3, вписан в конус.
Найдите высоту конуса, если радиус его основания равен Ответ: Реши задачу и оформи решение либо на альбомном листе, либо в виде электронного документа (PowerPoint, Paint, Word и т.д.) Что нового вы узнали на уроке? Домашнее задание Рефлексия Можете ли вы объяснить решение данных задач однокласснику, пропустившему урок сегодня? Чему вы научились? Какое у вас настроение в конце урока?
Использованные ресурсы 1. Стереометрические задачи и методы их решения.
А., Литвиненко В. Н., Мордкович А. Практикум по элементарной математике. М.: Просвещение, Комплект таблиц по стереометрии: 4. Единый государственный экзамен 2001: Тестовые задания: Математика/С.В.
Правильная Четырехугольная Пирамида
Стрункина, Е.И. Пантелеева и др.; М-во образования РФ. – М.: Просвещение, Для создания шаблона презентации использовалась картинка и шаблон с сайта 6. Рисунки на слайдах 6, 12, 13 взяты с сайта: ru/images/results.aspx?qu=%D1%81%D0%BC%D0%B0%D0%B9%D 0%BB%D1%8B ru/images/results.aspx?qu=%D1%81%D0%BC%D0%B0%D0%B9%D 0%BB%D1%8B.